Was
Correlation Charts: Revealing Hidden Relationships in Your Quality Data
Die Verteilung dieser Punkte ermöglicht es, Muster und Beziehungen visuell zu erkennen:
- Eine enge Gruppierung von Punkten entlang einer imaginären Linie deutet auf eine starke Korrelation hin.
- Je näher der Korrelationskoeffizient r bei +1 oder -1 liegt, desto stärker ist die Korrelation.
- Wenn r ≈ 0 ist, gibt es praktisch keine lineare Beziehung zwischen den Variablen.
- Die Richtung der Punktwolke zeigt an, ob die Korrelation positiv (aufsteigend) oder negativ (absteigend) ist.
Die Form der Punktwolke kann auch Aufschluss über nicht lineare Beziehungen geben, die der Korrelationskoeffizient allein nicht erfassen würde.
Wann
Korrelationsdiagramme werden in erster Linie verwendet, um den Grad und die Richtung des Zusammenhangs zwischen Variablen zu untersuchen. Mit ihrer Hilfe lässt sich feststellen, ob Veränderungen in einer Variablen mit Veränderungen in einer anderen korrespondieren, was sie für die Qualitätskontrolle, die Forschung und die Entscheidungsfindung unverzichtbar macht.
Typische Einsatzgebiete sind:
1. Qualitätskontrolle und Herstellung
Im Qualitätsmanagement werden Korrelationsdiagramme verwendet, um Faktoren zu ermitteln, die sich auf Produktfehler auswirken. Ein Fertigungsunternehmen könnte zum Beispiel die Korrelation zwischen der Geschwindigkeit der Produktionslinie und der Produktqualität analysieren, um seine Prozesse zu optimieren.
Sie helfen auch bei der Ursachenanalyse, indem sie aufzeigen, welche Variablen am stärksten mit Fehlern verbunden sind, was gezielte Verbesserungen ermöglicht.

2. Prädiktive Modellierung
Korrelationsdiagramme sind für die prädiktive Modellierung von Bedeutung. Korrelationen werden häufig von Modellen des maschinellen Lernens genutzt, um sicherzustellen, dass bei der Vorhersage eine relevante Auswahl von Merkmalen (Variablen) getroffen wird. Die Korrelation ist nützlich für die Auswahl der Merkmale und zur Verringerung der Multikollinearität in Regressionsmodellen.

3. Gesundheitswesen und Medizin
In der medizinischen Forschung zum Beispiel werden Korrelationskarten eingesetzt, um Zusammenhänge zwischen dem Altern des Kunden, dem Leben und dem Auftreten einer Krankheit zu untersuchen. Die Korrelationsanalyse wird häufig in klinischen Studien eingesetzt, um die Auswirkungen einer Behandlung auf eine Reihe von Patientenergebnissen zu bewerten.

Warum
Bei den Korrelationsdiagrammen geht es darum, die Beziehungen zwischen Variablen messbar und visuell darzustellen. Sie ermöglichen datengestützte Entscheidungen und Prognosen für die Zukunft auf der Grundlage historischer Daten.
Grundsätze
Action Management richtet sich nach den Gesetzen der:
Korrelationskoeffizienten: -1 bis 1
R - Die Korrelationskoeffizienten werden mit r bezeichnet und liegen auf einer Skala von -1 bis 1.
Ein r von -1 bedeutet, dass es eine perfekte negative Korrelation gibt - wenn die eine Sache steigt, sinkt die andere jedes Mal. Umgekehrt bedeutet ein "r" von 1 eine perfekte positive Korrelation, bei der beide Variablen perfekt zusammen steigen oder fallen.
Das heißt, wenn r = 0 ist, gibt es keine lineare Beziehung zwischen ihnen und sie sind daher unabhängig. Damit ist die Skala ein objektives und quantifizierbares Maß für die Stärke der Beziehung.
Dies führt dazu, dass Organisationen definieren können, was fehlerhaft ist oder was verbessert werden könnte, so dass eine effektive Planung und Ausführung zu einer Notwendigkeit wird - um alle Bemühungen auf effektive Ergebnisse auszurichten.

Korrelationskoeffizient: abhängig von der Art der Daten
Sie sollten wissen, welche Art von Korrelationskoeffizienten zu verwenden ist: Pearson für kontinuierliche und Spearman für ordinale Daten (z. B. ja/nein oder ok/nok).
Pearson prüft die Linearität der Daten, während Spearman im Gegensatz zu Pearson monotone Beziehungen in den Daten behandelt. Diese Option stellt sicher, dass die Art der Analyse, die wir durchführen, der Art der Daten entspricht, um bessere Ergebnisse zu erzielen.
Korrelation impliziert keine Kausalität
Eine Korrelation besagt lediglich, dass 2 Variablen miteinander in Beziehung stehen, und gibt keinen Hinweis darauf, wie diese kausal miteinander verbunden sein könnten. Daraus kann noch nicht geschlossen werden, dass die eine die andere verursacht, da zwei Variablen zwar eine Korrelation aufweisen können, aber möglicherweise in keiner Weise miteinander verbunden sind; dies könnte nur ein Zufall sein oder durch einen externen Faktor beeinflusst werden.
Kausalität - Es müssen kontrollierte Experimente durchgeführt werden (es können auch nur die Auswirkungen eines einzelnen Faktors untersucht werden), führt dies zu jenem usw. Die Korrelation hilft Ihnen, Zusammenhänge zu erkennen, nicht die Kausalität.
Wie
1. Sammeln Sie die Daten über die interessanten Variablen
Der erste Teil der Korrelationsanalyse besteht darin, die Daten für die zu betrachtenden Variablen zu beschaffen. Das bedeutet, dass man für jede Variable Datenpunkte (Beobachtungen) erhält und dass die Daten eine gute Repräsentation dessen sind, was man erreichen will; man braucht eine qualitativ hochwertige Datenerfassung, um die Korrelationen richtig und robust zu interpretieren.

2. Verwenden Sie einen Korrelationskoeffizienten basierend auf dem Datentyp
Wählen Sie den richtigen Korrelationskoeffizienten, um ein genaueres Ergebnis zu erhalten. Verwenden Sie den Pearson-Korrelationskoeffizienten für kontinuierliche Daten und den Spearman-Koeffizienten für ordinale (geordnete) Daten. Die Wahl sollte entsprechend der Eigenschaft der Daten getroffen werden, um die Beziehung effektiv zu erfassen.

3. Verwenden Sie eine Statistiksoftware, um den Korrelationskoeffizienten zu berechnen
Der Korrelationskoeffizient ist das Ergebnis einer mathematischen Operation, und wir werden in der Regel statistische Software oder Tabellenkalkulationsprogramme verwenden, um das Endergebnis zu berechnen, zum Beispiel Excel.
Die Verwendung dieser Werkzeuge verkürzt die Zeit und kann auch sicherstellen, dass der Korrelationskoeffizient korrekt berechnet wird.

4. Wie hoch ist der Koeffizient für die (positive, negative oder keine) Korrelation?
Die Interpretation des Korrelationskoeffizienten ist wichtig, um die Beziehung zwischen zwei Variablen zu erkennen.
Ein positiver Koeffizient bedeutet, dass eine positive Korrelation besteht: Wenn die unabhängige Variable zunimmt, nimmt auch die abhängige Variable tendenziell zu. Ein negatives Vorzeichen bedeutet, dass zwischen den beiden Variablen eine negative Korrelation besteht: Ein Anstieg der einen Variable führt zu einem Rückgang der anderen.
Es ist wichtig zu beachten, dass ein Koeffizient von 0 keine lineare Korrelation zwischen den Variablen anzeigt und somit Veränderungen in einer Variablen nicht systematisch mit Veränderungen in der anderen zusammenfallen.

5. Visualisieren Sie die Beziehung mithilfe eines Streudiagramms
Die Verwendung eines Streudiagramms zur Darstellung von Korrelationen ist ein wichtiger Bestandteil der Analyse. Diese Art von Diagramm gibt ein klares Bild davon, wie die Korrelation aussieht. Bei einer positiven Korrelation steigen die Punkte auf dem Streudiagramm in der Regel an, bei einer negativen Korrelation sinken sie. Liegt keine Korrelation vor, sind die Punkte ohne klares Muster verteilt. Diese Grafik hilft dabei, die Stärke der Korrelation und ihre Richtung zu erklären, und zeigt gleichzeitig Ausreißer oder seltsame Datenmuster auf.

Vorteile
Korrelationsdiagramme werden verwendet, um Variablen zu identifizieren, die Produktfehler im Qualitätsmanagement beeinflussen.
Dies eignet sich sehr gut für das Qualitätsmanagement und kann Korrelationsdiagramme erstellen, aus denen klar hervorgeht, welche Faktoren mehr Fehler pro Produkt verursachen. Auf diese Weise kann das Qualitätskontrollteam leicht feststellen, wo die Probleme auftreten, und kann (z. B.) anhand relevanter Produktionsparameter wie Materialqualität oder Maschinenleistung die Grundursachen für Fehler ermitteln. Anhand dieser Informationen können wir die notwendigen gezielten Maßnahmen ergreifen, um die Prozesse zu optimieren und letztendlich die Fehler zu reduzieren und die Qualität unserer Produkte zu sichern.

Prozessverbesserungen - mit Korrelationsdiagrammen, die zeigen, dass Qualitätsvariablen effiziente Prozesse fördern
Korrelationsdiagramme helfen bei der Prozessoptimierung – sie zeigen auf, welche Variablen die Qualität unserer Produkte beeinflussen. Unternehmen können die Qualität zurückentwickeln, indem sie die Variablen ermitteln, die am stärksten mit den gewünschten Qualitätsergebnissen verbunden sind, so dass sie diese Ressourcen für die Optimierung der Leistung bei diesen Faktoren einsetzen können. Da alle Verbesserungen in einem gemeinsamen Rahmen betrachtet werden sollten, wird sichergestellt, dass die Priorisierung auf der Grundlage realer Daten und nicht auf der Grundlage der Wahrnehmung potenzieller Auswirkungen auf die Qualität erfolgt, was die Abläufe effizienter und effektiver macht.

Entscheidungsträger können datengestützte Entscheidungen treffen, um Qualität und Effizienz zu verbessern
Korrelationsdiagramme ermöglichen es den Entscheidungsträgern, Entscheidungen auf der Grundlage von Benutzerdaten zu treffen. Dadurch können sie sowohl die Qualität als auch die Effizienz verbessern. Die Kenntnis der Beziehungen zwischen verschiedenen Prozessvariablen ermöglicht es Ihren Managern und Führungskräften, strategische Entscheidungen zu treffen, so dass sie eine hervorragende Produktqualität erhalten, ohne unnötige Ressourcen zu verbrauchen. Dies fördert eine bessere Nutzung der Ressourcen und eine Maximierung der betrieblichen Leistung insgesamt, was langfristige Vorteile für die Produktivitätsbilanz mit sich bringt.

Einschränkungen
Korrelation beweist keine Kausalität: externe Faktoren können beide Variablen beeinflussen
Eine Korrelationsanalyse impliziert keine Kausalität. Nur weil zwei Variablen stark miteinander korreliert sind, bedeutet das nicht, dass die eine die andere verursacht.
Um diesen Punkt weiter zu vertiefen, kann es auch versteckte oder verwirrende Variablen geben, die sowohl einzeln als auch zusammen eine Rolle spielen, so dass sie sich nicht nur direkt auf die Kausalität auswirken, sondern auch eine falsche Kausalbehauptung aufstellen können. Da es sich um eine Korrelationsstudie handelt, ist es wichtig, dass die Forscher ihre Interpretationen nicht über die Korrelationsebene hinaus ausdehnen. Solche Erkenntnisse bedürfen zukünftiger Forschung, um einen Kausalzusammenhang herzustellen.

Ausreißer können die Ergebnisse verzerren, was die Bedeutung der Datenbereinigung unterstreicht.
Die Korrelationsergebnisse können auch durch Ausreißer (Extremwerte, die sich stark vom Rest der Daten unterscheiden) dramatisch beeinflusst werden. Die oben erwähnten Verzerrungen können den berechneten Wert dieser Wunderzahl verfälschen und so zu unbegründeten Schlussfolgerungen führen. Um dies zu vermeiden, müssen Sie eine umfangreiche Datenbereinigung durchführen. Es ist daher wichtig, sie korrekt zu identifizieren und zu verwalten (ggf. umzuwandeln oder zu löschen), damit die Korrelationsanalyse eine genaue Beziehung zwischen den Variablen aufzeigen kann.
*** Übersetzt mit www.DeepL.com/Translator (kostenlose Version) ***

Die Korrelation reagiert empfindlich auf den Maßstab der Messung, was eine sorgfältige Prüfung erfordert.
Ein funktionierendes Maßnahmenmanagement wird durch eine starke Führung und Engagement in der gesamten Organisation unterstützt.
Wenn die Führung keine starke Unterstützung bietet, laufen die Programme Gefahr, blockiert zu werden, richtungslos zu sein oder an Fahrt zu verlieren. Die Führung ist der Schlüssel, um die Vision festzulegen, zu erklären, warum die Qualitätsverbesserung wichtig ist, und Ihnen angemessene Ressourcen und Befugnisse zu geben, um die Verbesserungen ordnungsgemäß durchzuführen.
Dies gilt auch für das Maßnahmenmanagement. Ohne eine solide Unterstützung durch die Führung können sie an Schwung verlieren und ihre Ziele nur schwer erreichen. Folglich ist eine gut funktionierende Führung, die sich nicht nur für die Ziele der Qualitätsverbesserung einsetzt, sondern auch mit ihnen übereinstimmt, für eine erfolgreiche Integration in die Organisationen unerlässlich.

Gute Praxis

Untersuchung der ursächlichen Faktoren neben der Korrelationsanalyse, um tiefere Einblicke zu gewinnen
Obwohl die Korrelationsanalyse bei der Ermittlung von Beziehungen zwischen Variablen helfen kann, ist es in der Regel interessant, ein wenig weiter zu gehen und potenzielle Kausalfaktoren zu untersuchen. Das Verständnis der Ursachen, die Korrelationen erzeugen, kann sehr aufschlussreich sein.
Wenn z. B. Mitarbeiter, die mehr Stunden trainieren, nachweislich produktiver sind, dann könnte es tatsächlich an der Qualität der Trainingsprogramme liegen. Darüber hinaus wird ein solches Verständnis gezieltere Eingriffe und Verbesserungen ermöglichen, die sich in Bereichen wie der Qualitätskontrolle oder der Prozessoptimierung positiv auswirken könnten.

Kontinuierliche Überwachung der Variablen zur Anpassung der Qualitätskontrollstrategien
Einer der wichtigsten Punkte im Qualitätsmanagement ist die kontinuierliche Überwachung der entsprechenden Variablen. Durch Korrelationsanalysen kann man Beziehungen zwischen Faktoren und Fehlern in Produkten beobachten, die sich jedoch im Laufe der Zeit ändern können.
Die kontinuierliche Erfassung und Analyse von Daten ist der Schlüssel dazu, dass Unternehmen ihre Strategien zur Qualitätskontrolle an die jeweiligen Umstände anpassen können. Die Prozesse werden auf der Grundlage neuer Korrelationsergebnisse so lange verfeinert, bis die "Wow"-Qualität erreicht ist.

Zeitreihenkorrelation nutzen, um Trends und saisonale Muster zu erkennen
Die Zeitreihenkorrelationsanalyse ist eine sehr wirksame Methode zur Ermittlung von Trends und saisonalen Mustern in Daten. Die Korrelation kann auf mit Zeitstempeln versehene Daten angewandt werden, z. B. auf die Anzahl der Defekte über Monate/Jahre hinweg - so können Sie vergangene Sequenzen sehen, die aufgetreten sind, und im Voraus über allgemeine Schwankungen nachdenken.
Diese Informationen ermöglichen eine bessere Ressourcenzuweisung, Bestandskontrolle und Produktionsplanung. Dies ist in jeder Branche von entscheidender Bedeutung, sei es in der Fertigung, im Einzelhandel oder in anderen Bereichen, da diese Art von Korrelationen den Entscheidungsträgern helfen, eine fundierte Entscheidung für einen reibungsloseren Betrieb zu treffen.
Beispiel
Beispiel 1: Starke negative Beziehung
Die Null-Fehler-Pizza-Pizzeria möchte wissen, ob eine Erhöhung der Ofentemperatur die Backzeit der Pizza linear verlängert, um eine Null-Fehler-Pizza zu erreichen. Es klingt, als würden sie vermuten, dass heißere Öfen kürzere Backzeiten bedeuten, aber sie brauchen einen konkreten Beweis.
Ziel:
Die Pizzeria möchte also ein Streudiagramm, um zu erklären, wie die Temperatur mit der Garzeit zusammenhängt, indem sie die Ofentemperatur auf einer Achse gegen die Backdauer auf einer y-Achse aufträgt, und um ein gewisses Maß an Stärke in diesem Zusammenhang zu gewinnen.

1. Daten sammeln
Um dies zu testen, sammelt die Pizzeria Daten, indem sie mehrere Pizzen bei verschiedenen Ofentemperaturen backt und die entsprechenden Backzeiten aufzeichnet, die erforderlich sind, um die gewünschte Krustenqualität zu erreichen.
Hier sind die Daten, die sie sammeln:
| Ofentemperatur (°C) | Backzeit (Minuten) |
|---|---|
| 210 | 14 |
| 220 | 13 |
| 230 | 12 |
| 240 | 11 |
| 250 | 10 |
| 260 | 9 |
| 270 | 8 |
| 280 | 7 |
2. Zeichnen Sie ein Korrelationsdiagramm
Sie stellen die Ofentemperatur auf der X-Achse und die Backzeit auf der Y-Achse dar, um zu sehen, ob es eine eindeutige Beziehung gibt:

3. Analysieren Sie die Beziehung
Anhand des sich daraus ergebenden Streudiagramms lässt sich feststellen, ob die beiden Variablen korreliert sind (z. B. eine negative Korrelation, wenn höhere Temperaturen zu kürzeren Backzeiten führen).
Hier zeigt das Korrelationsdiagramm die Beziehung zwischen Ofentemperatur und Backzeit. Das Streudiagramm stellt die gesammelten Datenpunkte dar, während die rote gestrichelte Linie den Trend (Best-Fit-Linie) zeigt, der die Korrelation angibt.
Analyse:
- Die Grafik zeigt eine negative Korrelation zwischen Ofentemperatur und Backzeit, d. h. mit steigender Ofentemperatur nimmt die Backzeit ab.
- Dieser Trend unterstützt die Hypothese der Pizzeria, dass höhere Temperaturen zu kürzeren Backzeiten führen.
Beispiel 2: Keine Beziehung
Jetzt will Zero-Defect Pizza herausfinden, ob es einen Zusammenhang zwischen der Größe der Pizza und der Kundenzufriedenheit gibt.
Sie vermuten, dass größere Pizzen zu einer höheren Kundenzufriedenheit führen, aber um dies zu bestätigen, sammeln sie Daten, indem sie Kunden, die verschiedene Pizzagrößen kaufen, befragen und sie bitten, ihre Zufriedenheit auf einer Skala von 1 bis 10 zu bewerten.
1. Erhobene Daten
| Pizza Größe (Zoll) | Kundenzufriedenheit (Skala 1-10) |
|---|---|
| 10 | 8 |
| 12 | 7 |
| 14 | 9 |
| 16 | 5 |
| 18 | 9 |
| 10 | 6 |
| 12 | 8 |
| 14 | 7 |
| 16 | 9 |
| 18 | 6 |
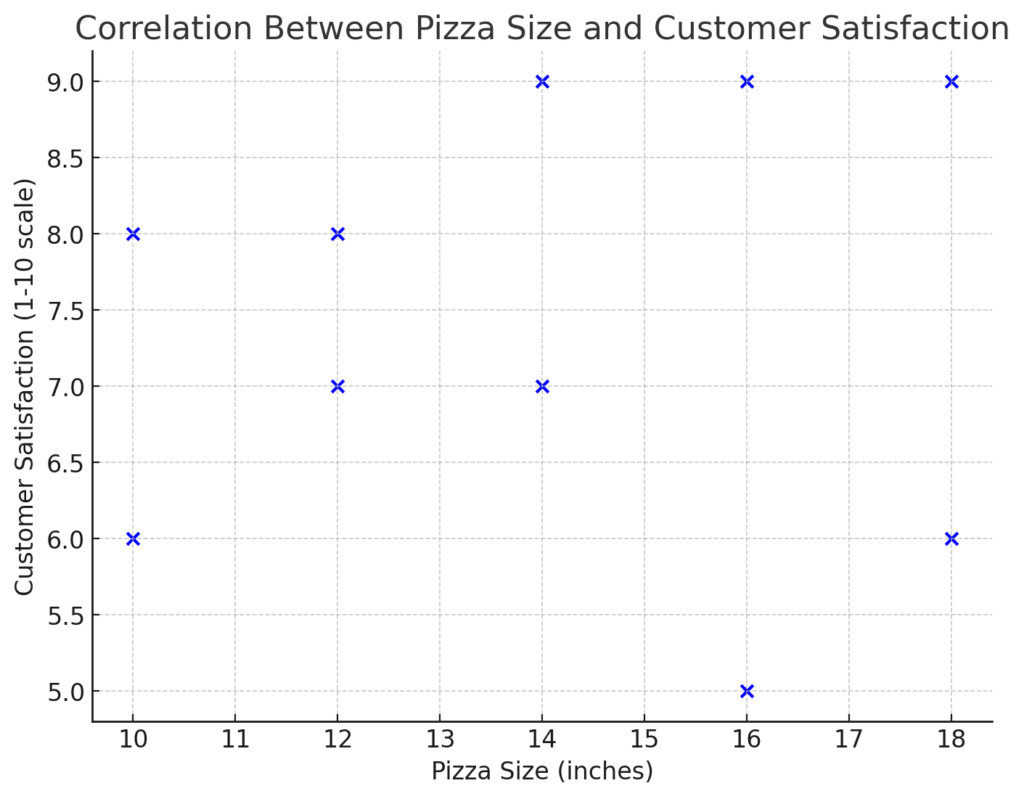
Nun werden die Daten unserer Pizzeria in einem Streudiagramm dargestellt, um zu sehen, ob ein eindeutiger Zusammenhang besteht:
2. Analyse
Das Streudiagramm zeigt, dass es keinen eindeutigen Zusammenhang zwischen Pizzagröße und Kundenzufriedenheit gibt. Die Datenpunkte sind verstreut und folgen keinem einheitlichen Muster, was bedeutet, dass die Kundenzufriedenheit in diesem Fall nicht von der Pizzagröße abzuhängen scheint.
FAQ
Was ist ein Korrelationsdiagramm?
Ein Korrelationsdiagramm ist eine grafische Darstellung, die zur Visualisierung der Beziehung zwischen zwei oder mehr Variablen verwendet wird. Mit ihrer Hilfe lässt sich feststellen, ob eine Beziehung besteht, wie stark sie ist und in welche Richtung sie geht (positive, negative oder keine Korrelation). Übliche Beispiele sind Streudiagramme und Heatmaps.
Was ist der r-Faktor in der Korrelationsanalyse?
Der r-Faktor, auch bekannt als Korrelationskoeffizient (Pearson’s r), ist ein numerischer Wert, der die Stärke und Richtung einer Beziehung zwischen zwei Variablen quantifiziert. Er reicht von -1 bis +1:
- +1: Perfekte positive Korrelation (wenn eine Variable steigt, steigt auch die andere).
- 0: Keine Korrelation (keine Beziehung zwischen den Variablen).
- -1: Perfekte negative Korrelation (wenn eine Variable steigt, sinkt die andere).
Wann wird eine Kollektivitätsanalyse durchgeführt?
Die Korrelationsanalyse wird in verschiedenen Szenarien durchgeführt, wie zum Beispiel:
- Wissenschaftliche Forschung zur Erforschung von Beziehungen zwischen Variablen.
- Wirtschaft und Finanzen, um Trends zu analysieren, z.B. Aktienkurse und Umsatzentwicklung.
- Gesundheitswesen, um die Beziehungen zwischen Lebensstilfaktoren und Gesundheitsergebnissen zu untersuchen.
- Engineering und Fertigung, um zu untersuchen, wie Prozessvariablen zusammenwirken.
Warum wird ein Korrelationsdiagramm verwendet?
Was sind die Prinzipien der Korrelationsanalyse?
Zu den wichtigsten Prinzipien der Korrelationsanalyse gehören:
- Richtung der Beziehung – Positive, negative oder keine Korrelation.
- Stärke der Beziehung – Wird anhand des Korrelationskoeffizienten gemessen.
- Kausalität vs. Korrelation – Korrelation bedeutet nicht gleich Kausalität.
- Datenzuverlässigkeit – Für aussagekräftige Ergebnisse sind genaue und ausreichende Daten erforderlich.
Wie wird eine Korrelationsanalyse durchgeführt?
Eine Korrelationsanalyse folgt diesen Schritten:
- Sammeln Sie Daten zu den Variablen, die Sie interessieren.
- Stellen Sie die Daten in einem Streudiagramm oder einer Heatmap dar.
- Berechnen Sie den Korrelationskoeffizienten (r) mithilfe statistischer Formeln oder Software.
- Interpretieren Sie die Ergebnisse, um die Stärke und Bedeutung der Beziehung zu bestimmen.
Was sind die Vorteile eines Korrelationsdiagramms?
- Bietet Einblicke in die Beziehungen zwischen Variablen.
- Hilft bei der Prognose und Vorhersage von Trends.
- Vereinfacht komplexe Datensätze in visuellen Darstellungen.
- Hilft bei der Entscheidungsfindung, indem er einflussreiche Faktoren identifiziert.
Was sind die Grenzen einer Korrelationsanalyse?
- Keine Kausalität Eine starke Korrelation bedeutet nicht, dass eine Variable die andere verursacht.
- Empfindlich gegenüber Ausreißern – Extreme Werte können die Ergebnisse verzerren.
- Misst nur lineare Beziehungen – Nicht-lineare Beziehungen werden möglicherweise nicht erkannt.
- Erfordert eine ausreichende Datenmenge – Kleine Datensätze können zu irreführenden Schlussfolgerungen führen.
Was sind die besten Praktiken der Korrelationsanalyse?
- Verwenden Sie eine angemessene Stichprobengröße, um Verzerrungen zu vermeiden.
- Suchen Sie nach Ausreißern und Anomalien, bevor Sie Schlussfolgerungen ziehen.
- Kombinieren Sie die Korrelation mit anderen statistischen Methoden, um tiefere Einblicke zu erhalten.
- Interpretieren Sie die Ergebnisse vorsichtig, damit Sie nicht von einer Kausalität ausgehen.
- Verwenden Sie geeignete Visualisierungstools wie Streudiagramme oder Heatmaps, um Klarheit zu schaffen.




